- Compare the graphs of the following functions to the graph of $y=x^{2}$.
(a) $y=x^{2}+2 x+3$
(b) $y=x^{2}-4 x+2$
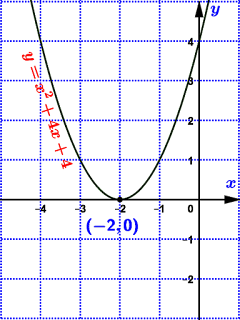
(c) $y=x^{2}+4 x+4$
- Compare the graphs of the following functions to the graph of $y=-x^{2}$.
(a) $y=-x^{2}+2 x+3$
(b) $y=-x^{2}-4 x-7$
(c) $y=-x^{2}+4 x-4$
Wednesday, July 14, 2021
Subscribe to:
Post Comments (Atom)

















0 Reviews:
Post a Comment