Exercise (4.5) - Rational Functions

Rational Functions

ပိုင်းဝေနှင့် ပိုင်းခြေ နှစ်ခုလုံး polynomial ဖြစ်နေသော အပိုင်းကိန်း ပုံစံကို rational function ဟုခေါ်သည်။ ဒဿမတန်း (သင်ရိုးသစ်) တွင် အခြေခံဖြစ်သည့် linear polynomial နှစ်ခု၏ အချိုးဖြင့်သာ ဖေါ်ပြသော rational function ပုံစံကိုသာ သင်ယူရမည် ဖြစ်သည်။

General Form	Asymptote Form
$ y=\displaystyle\frac{{ax+b}}{{cx+d}},\ x\ne -\displaystyle\frac{d}{c}$	$y=\displaystyle\frac{k}{{x-p}}+q,\ k\ne 0\ \text{and}\ x\ne p$

လက်တွေ့ graph ရေးဆွဲရာတွင် Asymptote Form က graph nature ကို လွယ်ကူစွာ ခန့်မှန်းနိုင်သည်။ ထို့ကြောင့် rational function တစ်ခုကို general form ဖြင့်ပေးထားလျှင် asymptote form သို့ ပြောင်းခြင်း အားဖြင့် graph ကို လွယ်ကူစွာ ရေးဆွဲနိုင်သည်။ asymptote form ၏ constant တစ်ခု ဖြစ်သော $k$ ၏ လက္ခဏာပေါ် မူတည်၍ rational function တစ်ခု ပုံစံကို အောက်ပါအတိုင်း ခွဲခြားနိုင်သည်။

Fig.1: Nature of the graph of $y=\displaystyle\frac{k}{{x-p}}+q,\ k> 0, \ \text{and}\ x\ne p$

Fig.2: Nature of the graph of $y=\displaystyle\frac{k}{{x-p}}+q,\ k< 0, \ \text{and}\ x\ne p$

General form $\displaystyle \frac{{ax+b}}{{cx+d}}$ မှ asymptote form $\displaystyle \frac{k}{{x-p}}+q$ သို့ အောက်ပါအတိုင်း ပြောင်းယူနိုင်ပါသည်။

$\begin{array}{l} \displaystyle\frac{{ax+b}}{{cx+d}}=\displaystyle\frac{k}{{x-p}}+q\\\\ \displaystyle\frac{{\displaystyle\frac{a}{c}x+\displaystyle\frac{b}{c}}}{{x+\displaystyle\frac{d}{c}}}=\displaystyle\frac{{qx+k-pq}}{{x-p}}\\\\ \text{Equating respective coefficients,}\\\\ q=\displaystyle\frac{a}{c},\ p=-\displaystyle\frac{d}{c}\\\\ k-pq=\displaystyle\frac{b}{c}\\\\ k=\displaystyle\frac{b}{c}+pq\\\\ k=\displaystyle\frac{b}{c}+\left( {-\displaystyle\frac{d}{c}} \right)\displaystyle\frac{a}{c}\\\\ k=\displaystyle\frac{{bc-ad}}{{{{c}^{2}}}}\\\\ \therefore \displaystyle\frac{{ax+b}}{{cx+d}}=\displaystyle\frac{{\displaystyle\frac{{bc-ad}}{{{{c}^{2}}}}}}{{x-\left( {-\displaystyle\frac{d}{c}} \right)}}+\displaystyle\frac{a}{c} \end{array}$

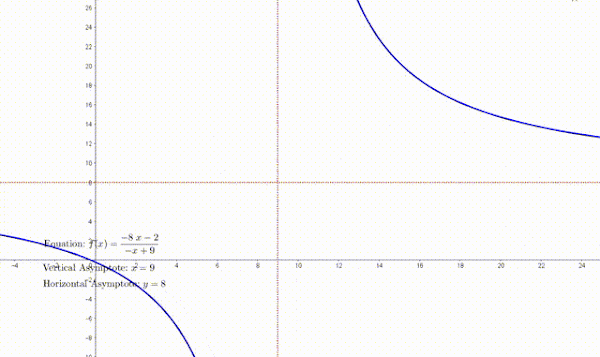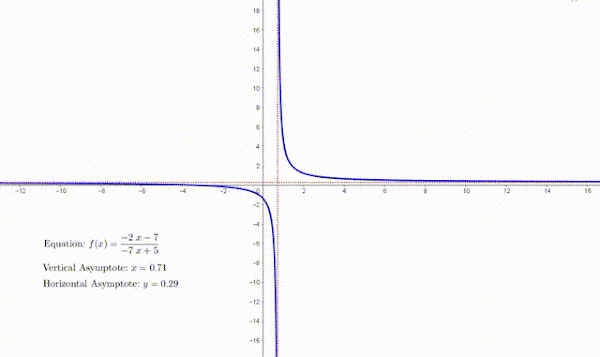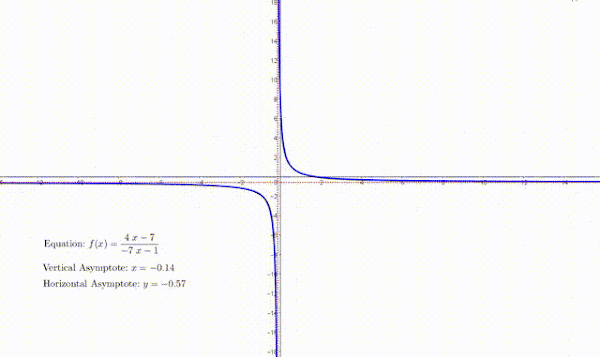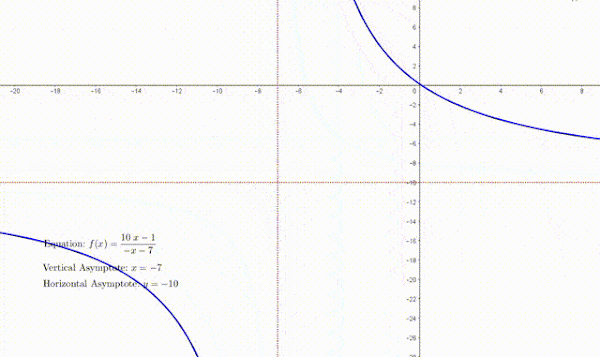
$ y=\displaystyle\frac{k}{{x-p}}+q$ ပုံစံတွင် $x$ ၏ ပမာန အလွန်ကြီးလာသည့် အခါ $y=\displaystyle\frac{k}{{x-p}}$ ပမာဏ အလွန်သေးငယ်သွားပြီး $0$ သို့ ချဉ်းကပ်သွားမည် ဖြစ်သည်။ သို့သော် $k \ne 0$ ဖြစ်သောကြောင့် $y=\displaystyle\frac{k}{{x-p}}$ သည် မည့်သည့်အခါမျှ $0$ နှင့် မညီပါ။ ထိုအခါ y သည်လည်း $q$ သို့ ချဉ်းကပ်သွားမည် ဖြစ်သည်။ ထိုသို့ graph က တဖြည်းဖြည်း ချဉ်းကပ်သွားသော ရေပြင်ညီမျဉ်း $y=q$ ကို horizontal asymptote ဟုခေါ်သည်။

အလားတူပင် $ y=\displaystyle\frac{k}{{x-p}}+q$ ပုံစံတွင် $p = 0$ ဖြစ်လျှင် function ကို define မလုပ်နိုင်သောကြောင့် $p ≠ 0$ ဖြစ်ရပါမည်။ သို့သော် $x$ သည် $p$ သို့ ချဉ်းကပ်သွားသည့်အခါ $ y=\displaystyle\frac{k}{{x-p}}+q$ သည် ပမာဏ ကြီးမားလာပြီး မည်၍မည်မျှရှိမည်ကို မသတ်မှတ်နိုင်သောကြောင့် အနန္တပမာဏ (infinity) ဟုသတ်မှတ်သည်။

• $x$ သည် $p$ နှင့် အလွန်နီးကပ်လာပြီး $p$ အောက် အနည်းငယ် ငယ်လျှင် $x \rightarrow p^{-}$ ဟုသတ်မှတ်သည်။ $p$ ၏ လက်ဝဲဘက်မှ ချဉ်းကပ်သည်ဟု ခေါ်သည်။


• $x$ သည် $p$ နှင့် အလွန်နီးကပ်လာပြီး $p$ ထက် အနည်းငယ် ကြီးလျှင် $x \rightarrow p^{+}$ ဟုသတ်မှတ်သည်။$p$ ၏ လက်ယာဘက်မှ ချဉ်းကပ်သည်ဟု ခေါ်သည်။


• $x \rightarrow p^{-}, k>0$, $y \rightarrow -\infty$


• $x \rightarrow p^{-}, k<0$, $y \rightarrow \infty$


• $x \rightarrow p^{+}, k>0$, $y \rightarrow \infty$


• $x \rightarrow p^{+}, k<0$, $y \rightarrow -\infty$

ထို့ကြောင့် graph က တဖြည်းဖြည်း ချဉ်းကပ်သွားသော ထောင်လိုက်မျဉ်း $x=p$ ကို vertical asymptote ဟုခေါ်သည်။

Graph ဆွဲရန်အတွက် $x$-intercept (when $y=0$) နှင့် $y$-intercept (when $x=0$) တို့ကို ရှာပေးရမည်။ ပေးထားသော function ပေါ်မူတည်၍ $x$-intercept နှင့် $y$-intercept မရှိသော အခြေအနေများလည်း တွေ့ရနိုင်ပါသည်။

Function တစ်ခု၏ domain ဆိုသည်မှာ အဆိုပါ function ကို define ဖြစ်စေသော x တန်းဖိုးများ အားလုံးပါဝင်သော အစုဖြစ်သည်။ $ y=\displaystyle\frac{k}{{x-p}}+q$ တွင် $x$ သည် $p$ ဖြင့် ညီခွင့် မရှိသောကြောင့် Domain = $\left\{ {x\ |\ x\ne p,x\in R} \right\}$ ဟု ပုံသေမှတ်ယူနိုင်သည်။ အလားတူပင် Function တစ်ခု၏ range ဆိုသည်မှာ image ($y$) များပါဝင်သော အစုဖြစ်သည်။ $y$ သည် $q$ ဖြင့် မည်သည့်အခါမျှ မညီနိုင်သောကြောင့် Range = $\left\{ {y\ |\ y\ne q,y\in R} \right\}$ ဟု ပုံသေမှတ်ယူနိုင်သည်။ ယခုရှင်းလင်းချက် အကြောင်းအရာတို့ကို ကောင်းစွာနားလည်ပြီးလျှင် exercise (4.5) ကို ဖြေရှင်းနိုင်ပြီ ဖြစ်သည်။

Exercise (4.5)

1. Sketch the graphs of the following functions.
   
   (a) $y=\displaystyle\frac{1}{x}$
   
   [Show Solution ]
   
   (b) $y=\displaystyle\frac{3}{x}$
   
   [Show Solution ]
   
   (c) $y=-\displaystyle\frac{2}{x}$
   
   [Show Solution ]
   
   (d) $y=-\displaystyle\frac{1}{2 x}$
   
   [Show Solution ]
   
   (e) $y=\displaystyle\frac{1}{3 x}$
   
   [Show Solution ]
   
   State the domain and range of each function.


2. Sketch the graphs of:
   
   (a) $y=-\displaystyle\frac{2}{x}+1$
   
   [Show Solution ]
   
   (b) $y=\displaystyle\frac{2}{x-3}$
   
   [Show Solution ]
   
   (c) $y=-\displaystyle\frac{1}{x+1}-1$
   
   [Show Solution ]
   
   (d) $y=\displaystyle\frac{2}{x+1}+2$
   
   [Show Solution ]
   
   State the domain and range of each function.


3. Sketch the graphs of:
   
   (a) $y=\displaystyle\frac{x+1}{x-1}$
   
   [Show Solution ]
   
   (b) $y=\displaystyle\frac{-3 x+4}{x-2}$
   
   [Show Solution ]
   
   (c) $y=\displaystyle\frac{2 x-3}{3 x+1}$
   
   [Show Solution ]
   
   State the domain and range of each function.