Circles - Definitions and Theorems (Part 1)

Circle and Centre of a Circle

A circle is the set of all points that are at a fixed distance from a fixed point. The fixed point producing a circle is called the centre of the circle.

A circle with centre $O$ is called circle $O$ and denoted by $\odot O$.

ရွေ့လျားမှုမရှိသော အမှတ်တစ်ခုမှ အကွာအဝေးတူ အမှတ်များဖြင့် ဖွဲ့စည်းထားသော အမှတ်အစုအဝေးကို စက်ဝိုင်းဟုခေါ်သည်။ စက်ဝိုင်းတစ်ခုကို ဖြစ်စေသည့် အဆိုပါ ရွေ့လျားမှုမရှိသော အမှတ်ကို ဗဟိုဟုခေါ်သည်။

$O$ ဗဟိုရှိသော စက်ဝိုင်းကို $\odot O$ ဟုခေါ်သည်။

Concentric Circles

Circles having the same centre are called concentric circles.

ဗဟိုတစ်ခုတည်းမှ ဖြစ်ပေါ်လာသော စက်ဝိုင်းများကို ဗဟိုတူစက်ဝိုင်းများ ဟုခေါ်သည်။

Radius

A radius is a segment joining the centre and a point on the circle.

ဗဟိုနှင့် စက်ဝန်းပေါ်ရှိ အမှတ်တစ်ခုကု ဆက်သွယ်ထားသော မျဉ်းပြတ်ကို အချင်းဝက် ဟုခေါ်သည်။

Chord

A segment joining two points on a circle is called a chord of the circle.

စက်ဝန်းပေါ်ရှိ အမှတ်နှစ်ခုကို ဆက်သွယ်ထားသော မျဉ်းပြတ်ကို လေးကြိုးဟု ခေါ်သည်။

Diameter

A diameter is a chord passing through the centre of a circle. In a circle, a diameter is a longest chord.

ဗဟိုကိုဖြတ်၍ဆွဲသော လေးကြိုးကို အချင်းမျဉ်းဟု ခေါ်သည်။ အချင်းမျဉ်းသည် စက်ဝိုင်းတစ်ခု၏ အရှည်းဆုံး လေးကြိုးလည်း ဖြစ်သည်။

Congruent Circles

Circles having the same radius are called congruent circles.

အချင်းဝက် တူညီသော စက်ဝိုင်းများကို ထပ်တူညီစက်ဝိုင်းများ ဟုခေါ်သည်။

Secant

A secant of a circle is a line that intersects the circle at two points.

စက်ဝန်းပေါ်ရှိ အမှတ်နှစ်ခုကို ဖြတ်သွားသော မျဉ်းတစ်ကြောင်းကိုဝန်းဖြတ်မျဉ်း ဟုခေါ်သည်။

Tangent

A line touching the circle at one point only is called a tangent to the circle. This touching point is called the point of contact.

စက်ဝိုင်းကို အမှတ်တစ်ခု၌ ထိသွားသော မျဉ်းတစ်ကြောင်းကို ဝန်းထိမျဉ်း ဟုခေါ်သည်။

Arc, Semicircle, Minor Arc, Major Arc

An arc is a part of a circle.

စက်ဝိုင်း၏ အစိပ်အပိုင်းကို အဝန်းပိုင်း ဟုခေါ်သည်။

A semicircle is a half part of a circle.

စက်ဝိုင်း၏ တစ်ဝက်တိတိရှိသော အစိပ်အပိုင်းကို စက်ဝိုင်းခြမ်း ဟုခေါ်သည်။

Arc $ACB$ is a semicircle.

A minor arc is an arc shorter than a semicircle.

စက်ဝိုင်းခြမ်းအောက် အလျားတိုသော အဝန်းပိုင်းကို minor arc ဟုခေါ်သည်။

A major arc is an arc longer than a semicircle.

စက်ဝိုင်းခြမ်းထက် အလျားရှည်သော အဝန်းပိုင်းကို major arc ဟုခေါ်သည်။

Arc $AB$ is a minor arc and arc $ACB$ is a major arc.

Central Angles and Inscribed Angles

A central angle is an angle subtended by an arc (or chord) of a circle at the centre.

ထောင့်လက်တံနှစ်ခု၏ အစွန်းမှတ်များသည် အဝန်းပိုင်း၏ အစွန်းနှစ်ဘက် (သို့မဟုတ်) လေးကြိုး၏ အစွန်းနှစ်ဘက်၌ ရှိပြီး ထောင်းစွန်းမှတ်သည် စက်ဝိုင်းတစ်ခု၏ ဗဟို၌ရှိသော ထောင့်ကို ဗဟိုခံထောင့်ဟု ခေါ်သည်။

An inscribed angle is an angle subtended by an arc (or chord) of a circle at a point on the other arc.

ထောင့်လက်တံနှစ်ခု၏ အစွန်းမှတ်များသည် အဝန်းပိုင်း၏ အစွန်းနှစ်ဘက် (သို့မဟုတ်) လေးကြိုး၏ အစွန်းနှစ်ဘက်၌ ရှိပြီး ထောင်းစွန်းမှတ်သည် စက်ဝိုင်းတစ်ခု၏ အဝန်း၌ရှိသော ထောင့်ကို အဝန်းခံထောင့်ဟု ခေါ်သည်။

Theorem 1

The central angle is twice the inscribed angle subtended by the same arc.

အဝန်းပိုင်းတစ်ခုမှ စက်ဝိုင်း၏ ဗဟိုတွင်ခံဆောင်ထားသော ထောင့်သည် အဆိုပါအဝန်းပိုင်းကိုပင် တစ်ဖက်အဝန်းပိုင်းတွင် ခံဆောင်ထားသော ထောင့်၏ နှစ်ဆရှိသည်။

Visual Proof

Corollary 1.1

Inscribed angles subtended by the same arc are equal.

တူညီသော အဝန်းပိုင်းတစ်ခုမှ အခြားအဝန်းပိုင်းတစ်ခုတွင် ခံဆောင်ထားသော အဝန်းခံထောင့်များ တူညီကြသည်။

Visual Proof

Corollary 1.2

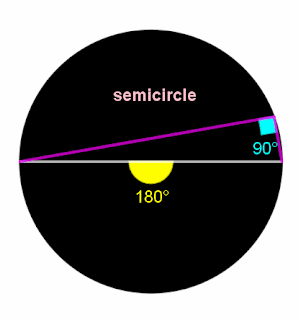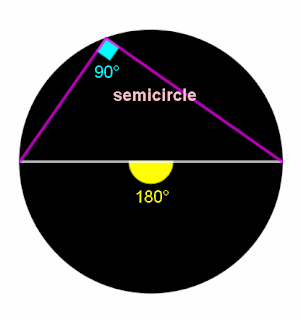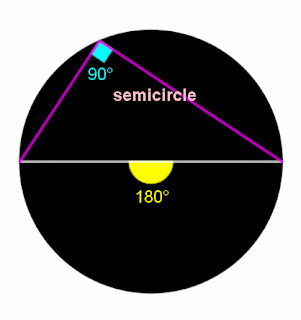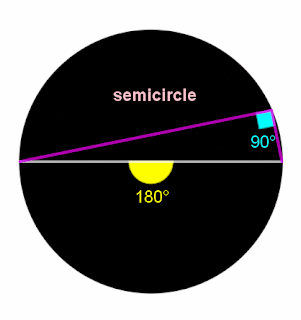
An inscribed angle subtended by a diameter is a right angle.

အချင်းမျဉ်းကို အဝန်းပိုင်း၌ ခံဆောင်ထားသော အဝန်းခံထောင့်သည် ထောင့်မှန်တစ်ခု ဖြစ်သည်။

Cyclic Quadrilateral

A quadrilateral whose vertices lie on a circle is called a cyclic quadrilateral.

စက်ဝိုင်းပေါ်တွင် ထောင့်စွန်းမှတ်များရှိသော စတုဂံတစ်ခုကို စက်ဝိုင်းတွင်းကျစတုဂံ ဟုခေါ်သည်။

$ABCD$ is a cyclic quadrilateral.

Theorem 2

Opposite angles of a cyclic quadrilateral are supplementary.

စက်ဝိုင်းတွင်းကျစတုဂံ စတုဂံတစ်ခု၏ အတွင်းမျက်နှာချင်းဆိုင် ထောင့်တစ်စုံသည် ထောင့်ဖြောင့်ဖြည့်ဘက်များ ဖြစ်ကြသည်။

Corollary 2.1

The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle of the quadrilateral

စက်ဝိုင်းတွင်းကျစတုဂံ စတုဂံတစ်ခု၏ အနားတစ်ဖက်ကို ဆက်ဆွဲ၍ ဖြစ်ပေါ်လာသော အပြင်ထောင့်သည် အတွင်းမျက်နှာချင်းဆိုင်ထောင့်နှင့် အမြဲ‌ညီသည်။

Theorem 3

In the same circle or in congruent circles,

1. equal arcs subtend equal central angles,
2. arcs subtending equal central angles are equal.

စက်ဝိုင်းတစ်ခုတည်းတွင် ဖြစ်စေ၊ ထပ်တူညီသော စက်ဝိုင်းများတွင် ဖြစ်စေ၊ အဝန်းပိုင်းများ ထပ်တူညီလျှင် ဗဟိုခံထောင့်များ တူညီပြီး၊ အပြန်အလှန်အားဖြင့် ဗဟိုခံထောင့်များ တူညီလျှင် အဝန်းပိုင်းများ ထပ်တူညီသည်။

Theorem 4

In the same circle or in congruent circles, two inscribed angles are equal if and only if the corresponding arcs are equal.

စက်ဝိုင်းတစ်ခုတည်းတွင် ဖြစ်စေ၊ ထပ်တူညီသော စက်ဝိုင်းများတွင် ဖြစ်စေ၊ အဝန်းပိုင်းများ ထပ်တူညီလျှင် အဝန်းခံထောင့်များ တူညီပြီး၊ အပြန်အလှန်အားဖြင့် အဝန်းခံထောင့်များ တူညီလျှင် အဝန်းပိုင်းများ ထပ်တူညီသည်။