1. Sketch the graphs of:
$\begin{array}{l} \text{(a)}\ \ \ y=x-1\\\\ \text{(b)}\ \ \ y=-x-2\\\\ \text{(c)}\ \ \ y=-x+2\\\\ \text{(d)}\ \ \ y=2 x+1\\\\ \text{(e)}\ \ \ y=3 x^{2}\\\\ \text{(f)}\ \ \ y=-3 x^{2}\\\\ \text{(g)}\ \ \ y=\frac{1}{3} x^{2}\\\\ \text{(h)}\ \ \ y=\sqrt{2 x}\\\\ \text{(a)}\ \ \ y=|2 x|\\\\ \end{array}$
(a) $y=x-1$
Show/Hide Solution
Firstly, we have to construct a table of order pair $(x,y)$ for the graph $y=x-1$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=x-1 & \ldots & -4 & -3 & -2 & -1 & 0 & 1 & 2 & \ldots \\ \hline \end{array}$
(b) $y=-x-2$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=-x-2$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=-x-2 & \ldots & 1 & 0 & -1 & -2 & -3 & -4 & -5 & \ldots \\ \hline \end{array}$
(c) $y=-x+2$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=-x+2$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=-x+2 & \ldots & 5 & 4 & 3 & 2 & 1 & 0 & -1 & \ldots \\ \hline \end{array}$
(d) $y=2x+1$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=2x+1$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=2x+1 & \ldots & -5 & -3 & -1 & 1 & 3 & 5 & 7 & \ldots \\ \hline \end{array}$
(e) $y=3x^2$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=3x^2$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=3x^2 & \ldots & 27 & 12 & 3 & 0 & 3 & 12 & 27 & \ldots \\ \hline \end{array}$
(f) $y=-3x^2$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=-3x^2$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=-3x^2 & \ldots & -27 & -12 & -3 & 0 & -3 & -12 & -27 & \ldots \\ \hline \end{array}$
(g) $y=\displaystyle\frac{1}{3}x^2$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=\displaystyle\frac{1}{3}x^2$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=\displaystyle\frac{1}{3}x^2 & \ldots & 3 & \displaystyle\frac{4}{3} & \displaystyle\frac{1}{3} & 0 & \displaystyle\frac{1}{3} & \displaystyle\frac{4}{3} & 3 & \ldots \\ \hline \end{array}$
(h) $y=\sqrt{2x}$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=\sqrt{2x}$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & 0 & 1 & 2 & 3 & 4 & 6 & 6 & \ldots \\ \hline y=y=\sqrt{2x} & \ldots & 0 & \sqrt{2} & 2 & \sqrt{6} & 2\sqrt{2} & \sqrt{10} & 2\sqrt{3} & \ldots \\ \hline \end{array}$
(i) $y=|2x|$
Show/Hide Solution
Firstly, we have to construct a table for order pair $(x,y)$ for the graph $y=|2x|$ and plotting them on the cartesian plane. Then join the points with smooth curve to illustrate the required graph.
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=|2x| & \ldots & 6 & 4 & 2 & 0 & 2 & 4 & 6 & \ldots \\ \hline \end{array}$
Grade 10 ဟာ function ရဲ့ အခြေခံသဘောကို သင်ကြားတာ ဖြစ်ပါတယ်။ ဒါကြောင့် ကျောင်းသူကျောင်းသားများ အနေဖြင့် function တစ်ခုကို graph ဆွဲတဲ့အခါ graph paper ကို သုံးရပါမယ်။ graph paper မသုံးပဲဆွဲလို့မရဘူးဆိုတော့ ရပါတယ်။ graph တစ်ခုတည်းမဟုတ်ပဲ graph များစွာဆွဲရန် လိုအပ်တဲ့အခါ graph paper သုံးပြီး ဆွဲမှသာ အဆင်ပြေပါတယ်။
သဘောတရားပဲ ဆွဲပြရင်မရဘူးလားလို့ စောဒက တက်စရာရှိပါတယ်။ function တစ်ခုရဲ့ သဘောတရားနဲ့ သဘောသဘာ၀ကို သိဖို့ ကျောင်းသားတစ်ယောက်နေနဲ့ $(x, y)$ order pair တွေကို များနိုင်သမျှ များများရှာထားမှသာ အဆင်ပြေပါတယ်။ ယေဘုယျ ပြောရရင်တော့ grade 10 အဆင့် သင်ခန်းစာတွေမှာ domain က real number ဖြစ်တဲ့အခါ integer subset တစ်ခု ဖြစ်တဲ့ $\{-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 \}$ ထည့်ဆွဲမယ်ဆိုရင် function ရဲ့ nature ကို ပေါ်လွင်စေနိုင်ပါတယ်။...
2. Sketch the graphs of $y =2x$ and $y =\displaystyle\frac{1}{2}x$ in the same plane. What do you notice from the graphs? Explain.
Show/Hide Solution
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=2x & \ldots & -6 & -4 & -2 & 0 & 2 & 4 & 6 & \ldots \\ \hline \end{array}$
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=\displaystyle \frac{1}{2}x & \ldots & -\displaystyle \frac{3}{2} & -1 & -\displaystyle \frac{1}{2} & 0 & \displaystyle \frac{1}{2} & 1 & \displaystyle \frac{3}{2} & \ldots \\ \hline \end{array}$
- Both are linear functions.
- Both graphs are straight lines.
- Both are increasing, i.e., both have positive slopes.
- Both passes through the origin.
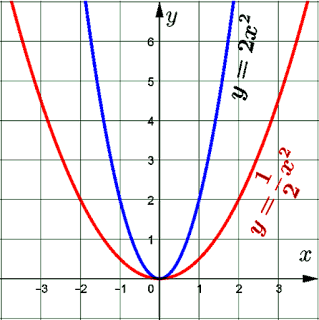
3. Sketch the graphs of $y =\displaystyle \frac{1}{2}x^2$ and $y =2x^2$ in the same plane. What do you notice from the graphs? Explain.
Show/Hide Solution
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=\displaystyle \frac{1}{2}x^2 & \ldots & \displaystyle \frac{9}{2} & 2 & \displaystyle \frac{1}{2} & 0 & \displaystyle \frac{1}{2} & 2 & \displaystyle \frac{9}{2} & \ldots \\ \hline \end{array}$
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline x & \ldots & -3 & -2 & -1 & 0 & 1 & 2 & 3 & \ldots \\ \hline y=2x^2 & \ldots & 18 & 8 & 2 & 0 & 2 & 8 & 18 & \ldots \\ \hline \end{array}$
- Both are quadratic functions.
- Both graphs are parabolas.
- Both are opening upward.
- Both functions have vertices at the origin.























0 Reviews:
Post a Comment