1. If 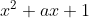 is a factor of
is a factor of 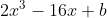 , Find the values of
, Find the values of  and
and 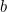 .
.
Solution
Let=2x%5E3-16x+b) .
.
Since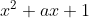 is a factor of
is a factor of ) , the remainder when
, the remainder when 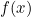 is divided by
is divided by 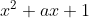 is 0.
is 0.
By polynomial long division we can find the remainder.
Hence we havex&space;+&space;2a&space;+&space;b&space;=0) .
.
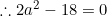
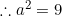 and
and 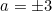 .
.
Similarly, we can say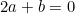 ,
,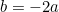
When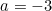 ,
, 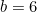 and
and
When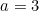 ,
, 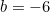 .
.
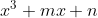 is divisible by
is divisible by %5E2) , prove that
, prove that %5E3+%5Cleft&space;(&space;%5Cfrac%7Bn%7D%7B2%7D&space;%5Cright&space;)%5E2=0) .
.
Solution
Since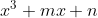 is divisible by
is divisible by 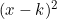 , The remainder when
, The remainder when 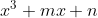 is divided by
is divided by 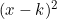 =
= 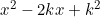 is zero.
is zero.
By polynomial long division,
 and
and 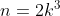 .
.
%5E3+%5Cleft&space;(&space;%5Cfrac%7Bn%7D%7B2%7D&space;%5Cright&space;)%5E2=%5Cleft&space;(%5Cfrac%7B&space;-3k%5E2%7D%7B3%7D&space;%5Cright&space;)%5E3+%5Cleft&space;(&space;%5Cfrac%7B2k%5E3%7D%7B2%7D&space;%5Cright&space;)%5E2=-k%5E6+k%5E6%3D0) .
.
Solution
Let
Since
By polynomial long division we can find the remainder.
Hence we have
Similarly, we can say
When
When
-------------------------------------------------------------------------
2. If Solution
Since
By polynomial long division,