Integration နှင့် ပတ်သက်ပြီး အောက်ပါ သင်ခန်းစာ များကို ရေးသားခဲ့ပါသည်။ ယခုသင်ခန်းစာကို ဖော်ပြပါသင်ခန်းစာများနှင့် တွဲဖက်လေ့လာရမည် ဖြစ်ပါသည်။
- AREA UNDER A CURVE
- ANTI-DERIVATIVE
- PRACTICE PROBLEMS FOR INDEFINITE INTEGRATION
- INTEGRATION OF $\dfrac{1}{x}$ AND $\dfrac{1}{ax+b}$ EXPONENTIAL FUNCTION
- INTEGRATION BY SUBSTITUTION
- INDEFINITE INTEGRATION
Problems
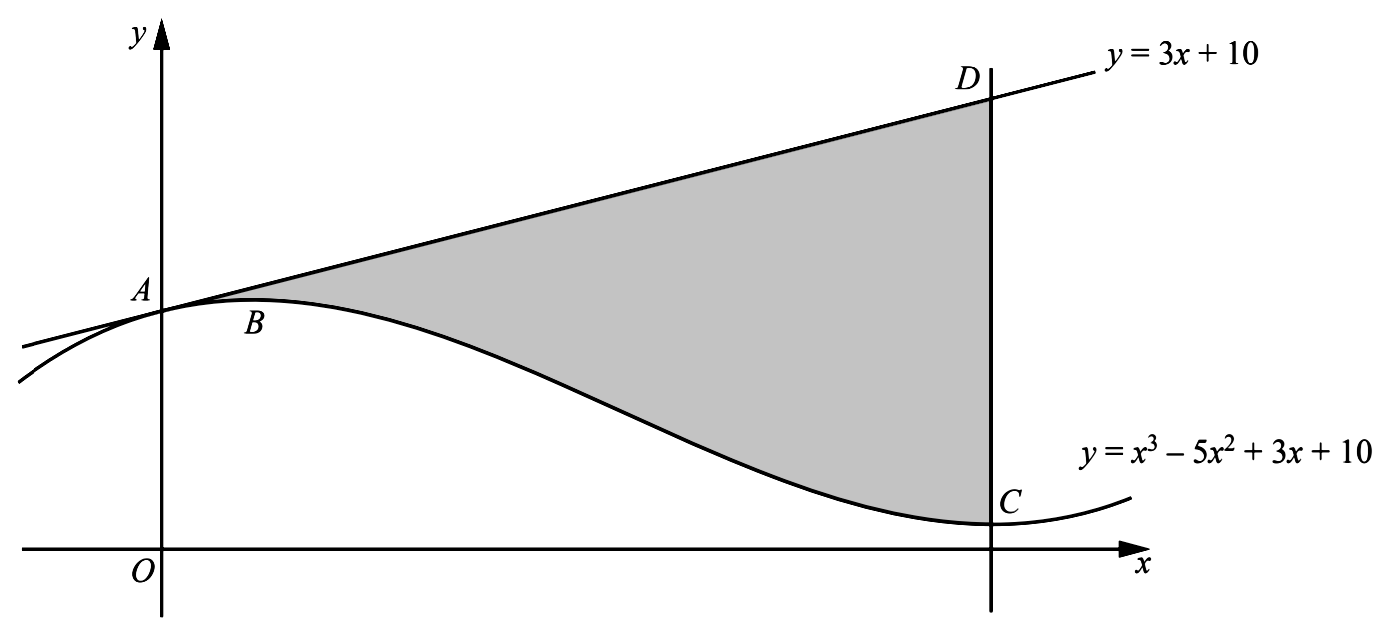
- The diagram shows parts of the line $y=3 x+10$ and the curve $y=x^{3}-5 x^{2}+3 x+10$. The line and the curve both pass through the point $A$ on the $y$ -axis. The curve has a maximum at the point $B$ and a minimum at the point $C$. The line through $C$, parallel to the $y$ -axis, intersects the line $y=3 x+10$ at the point $D$.
- Show that the line $A D$ is a tangent to the curve at $A$.
- Find the $x$ -coordinate of $B$ and of $C$.
- Find the area of the shaded region $A B C D$, showing all your working.
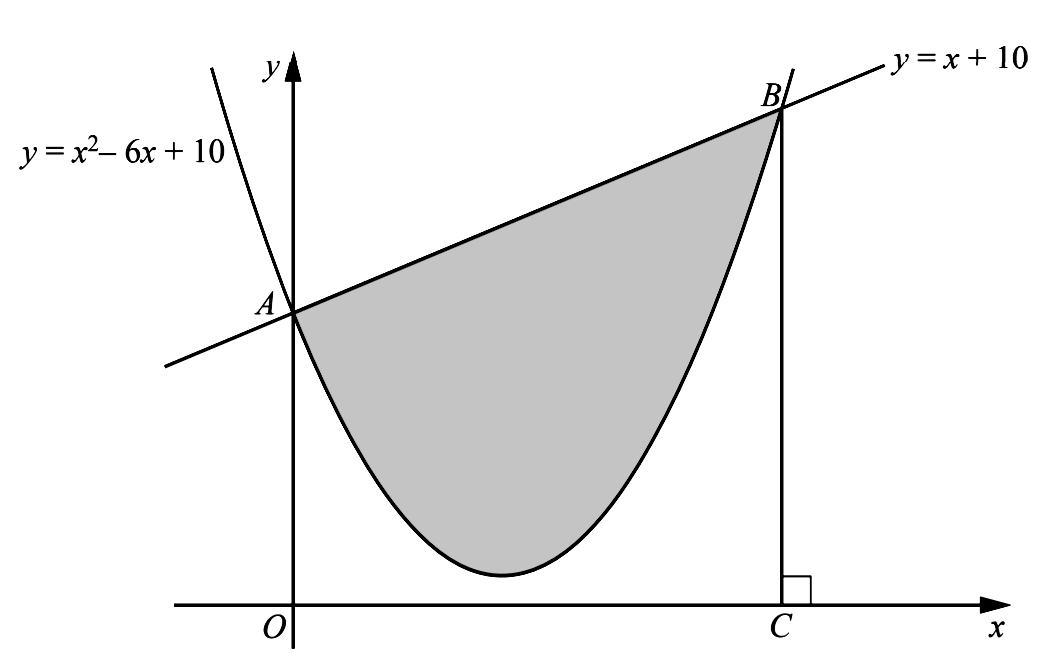
- The graph of $y=x^{2}-6 x+10$ cuts the $y$ -axis at $A$. The graphs of $y=x^{2}-6 x+10$ and $y=x+10$ cut one another at $A$ and $B$. The line $B C$ is perpendicular to the $x$ -axis. Calculate the area of the shaded region enclosed by the curve and the line $A B$, showing all your working.
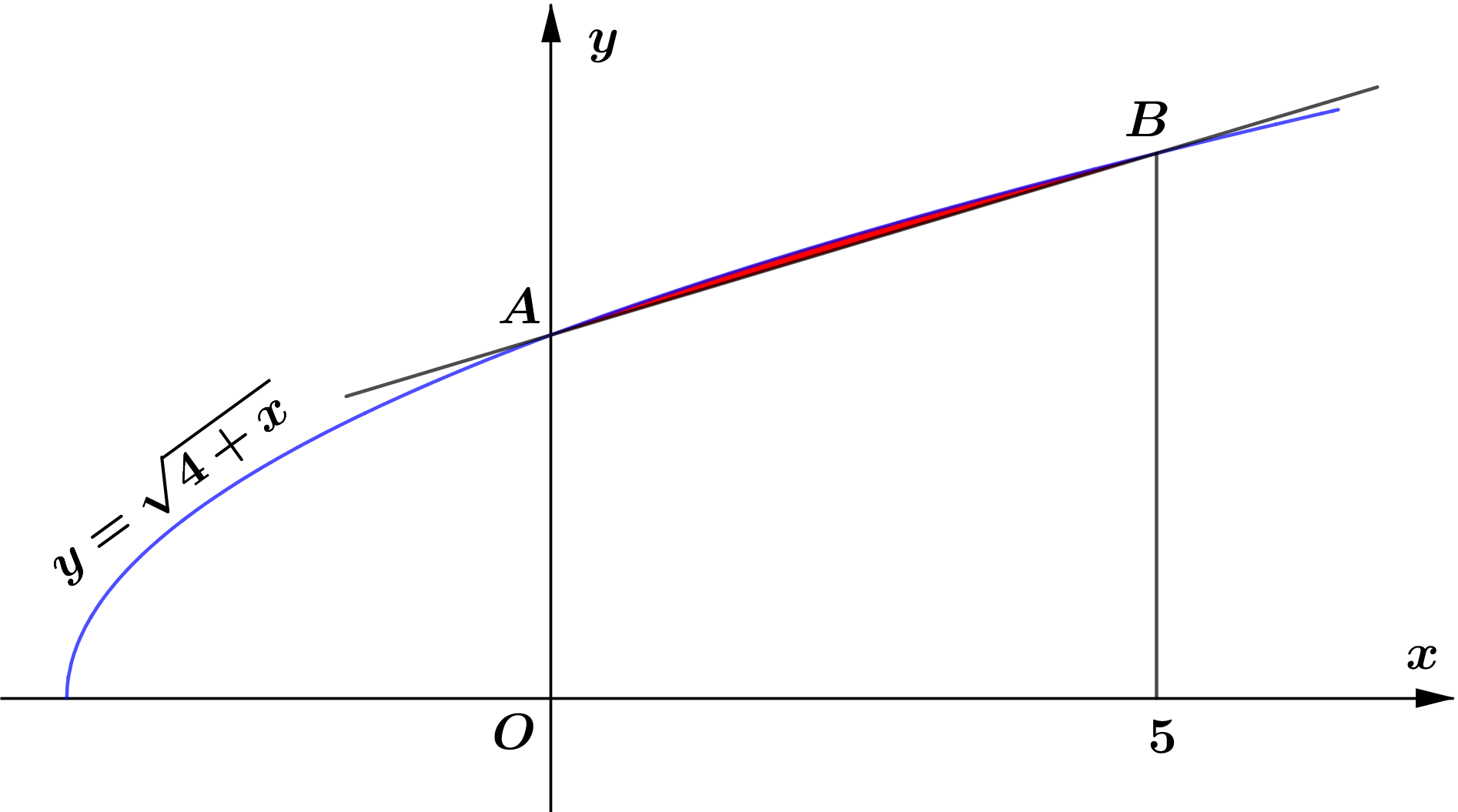
- The diagram shows the graph of $y=\sqrt{4+x}$, which meets the $y$ -axis at the point $A$ and the line $x=5$ at the point $B$. Find the area of the region enclosed by the curve and the straight line $A B$.
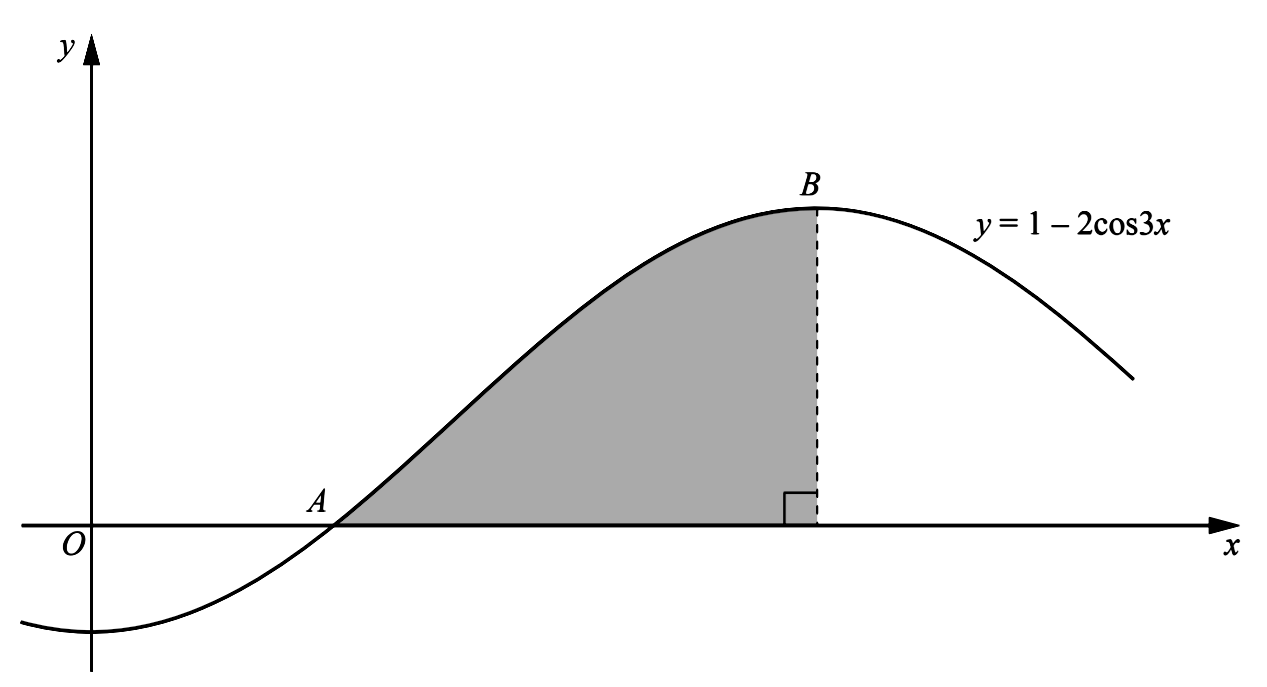
- The diagram shows part of the graph of $y=1-2 \cos 3 x$, which crosses the $x$ -axis at the point $A$ and has a maximum at the point $B$.
- Find the coordinates of $A$.
- Find the coordinates of $B$.
- Showing all your working, find the area of the shaded region bounded by the curve, the $x$ -axis and the perpendicular from $B$ to the $x$ -axis.
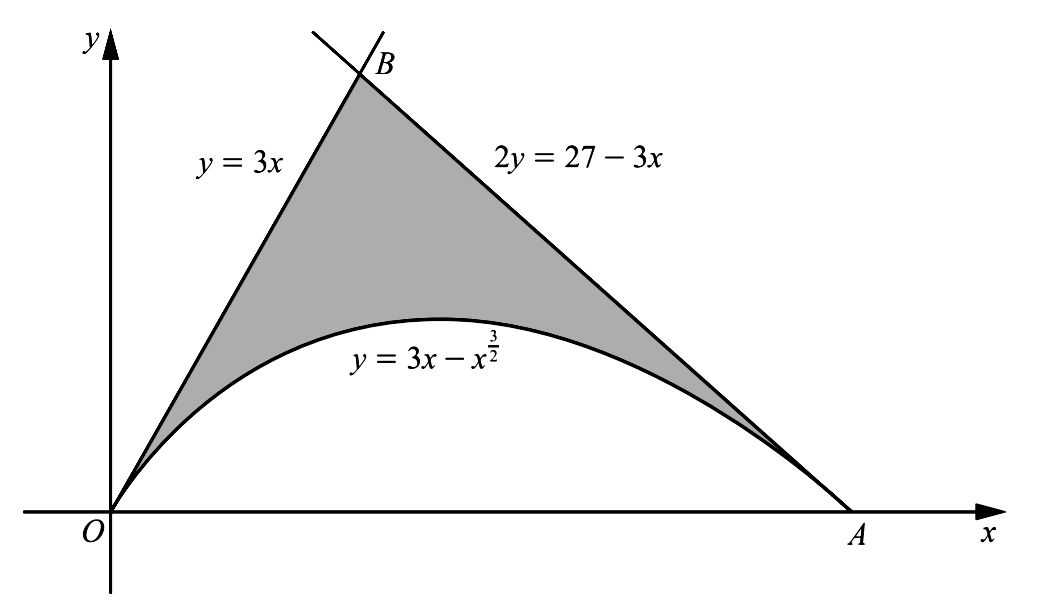
- The diagram shows part of the curve $y=3 x-x^{\frac{3}{2}}$ and the lines $y=3 x$ and $2 y=27-3 x$. The curve and the line $y=3 x$ meet the $x$ -axis at $O$ and the curve and the line $2 y=27-3 x$ meet the $x$ -axis at $A$.
- Find the coordinates of $A$.
- Verify that the coordinates of $B$ are $(3,9)$
- Find the area of the shaded region.
- The diagram shows part of the graph of $y=2 \cos \left(x-\dfrac{\pi}{6}\right)$. The graph intersects the $y$ -axis at the point $A$, has a maximum point at $B$ and intersects the $x$ -axis at the point $C$.
- Find the coordinates of $A$.
- Find the coordinates of $B$.
- Find the coordinates of $C$.
- Find $\displaystyle\int 2 \cos \left(x-\dfrac{\pi}{6}\right) \mathrm{d} x$.
- Hence find the area of the shaded region.
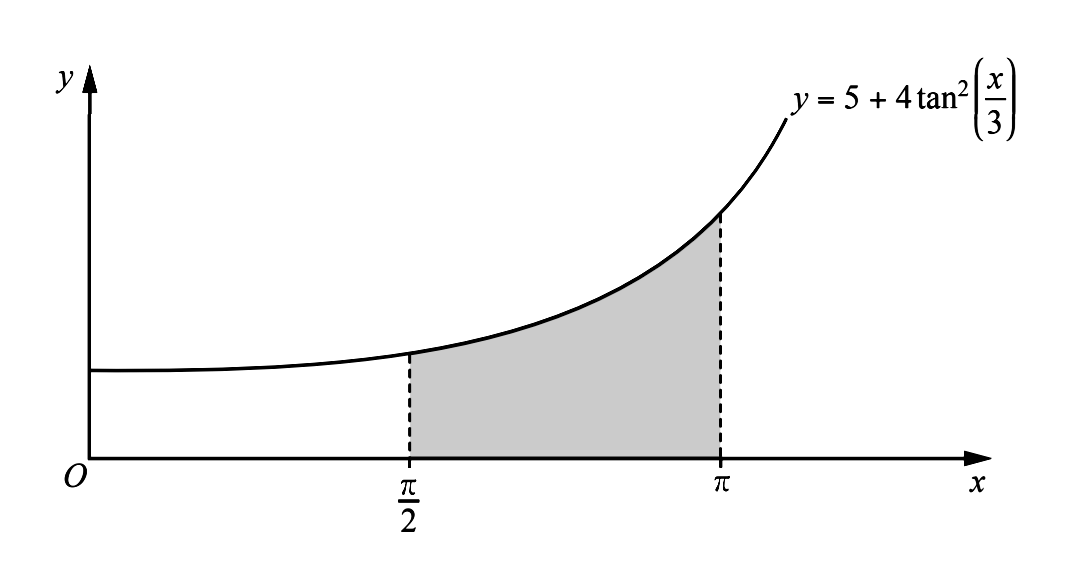
- The diagram shows part of the curve $y=5+4 \tan ^{2}\left(\dfrac{x}{3}\right)$. Hence, find the exact area of the shaded region enclosed by the curve, the $x$ -axis and the lines $x=\dfrac{\pi}{2}$ and $x=\pi$
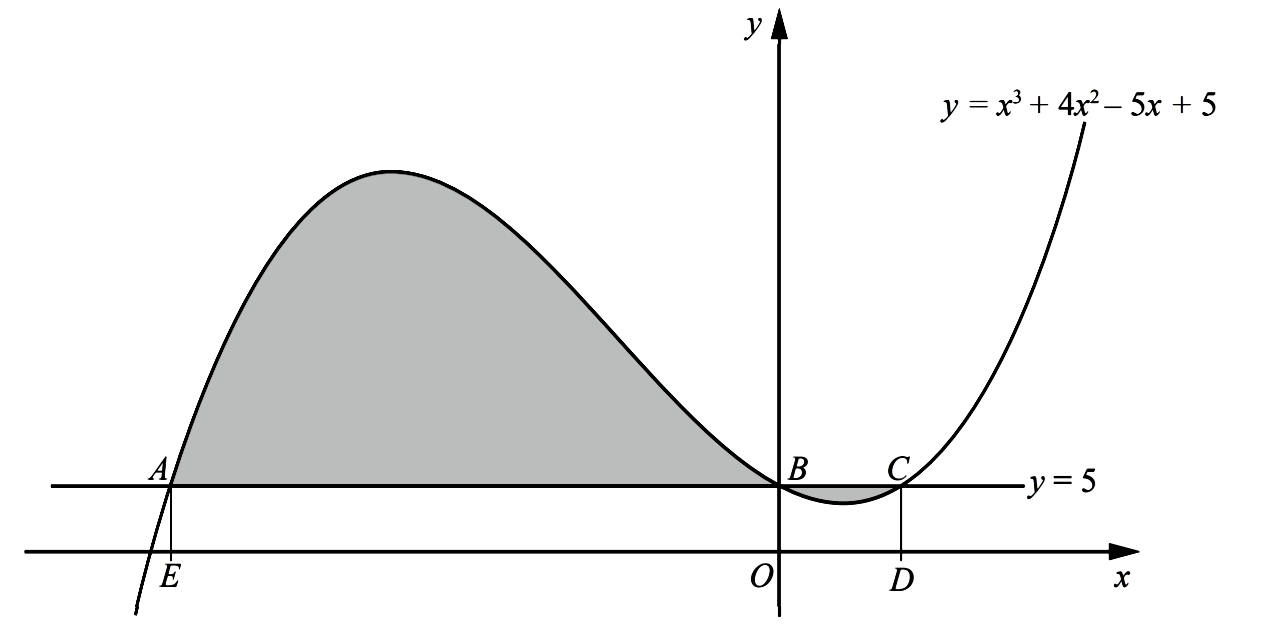
- The diagram shows part of the curve $y=x^{3}+4 x^{2}-5 x+5$ and the line $y=5$. The curve and the line intersect at the points $A, B$ and $C .$ The points $D$ and $E$ are on the $x$ -axis and the lines $A E$ and $C D$ are parallel to the $y$ -axis.Calculate the total area of the shaded regions enclosed between the line and the curve. You must show all your working.
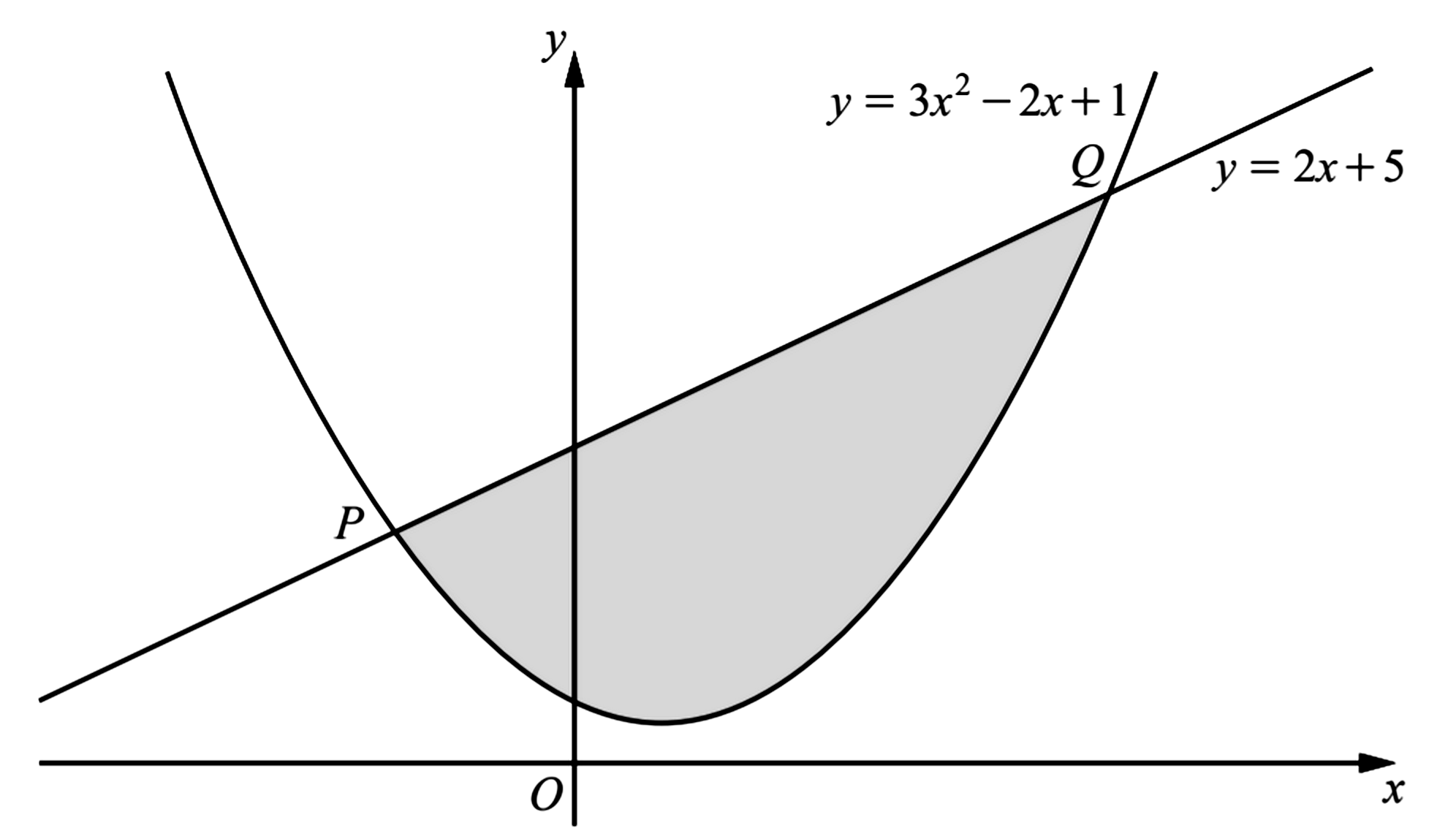
- The diagram shows the curve $y=3 x^{2}-2 x+1 $ and the straight line $y=2 x+5$ intersecting at the points $P$ and $Q$. Showing all your working, find the area of the shaded region.
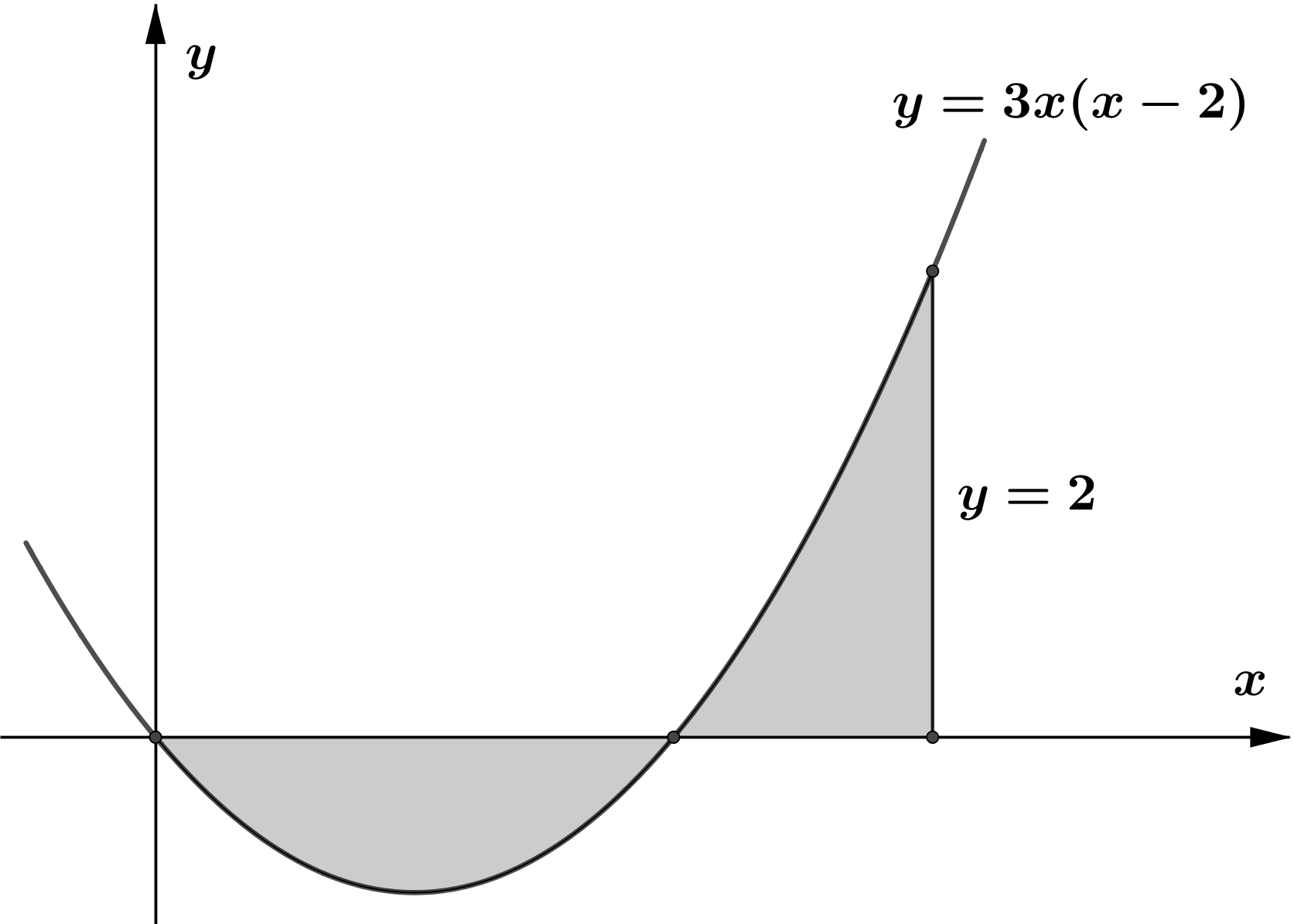
- The figure shows part of the curve $y=3 x(x-2) .$ Find the total area enclosed by the curve $y=3 x(x-2)$, the $x$ -axis and the line $x=3$
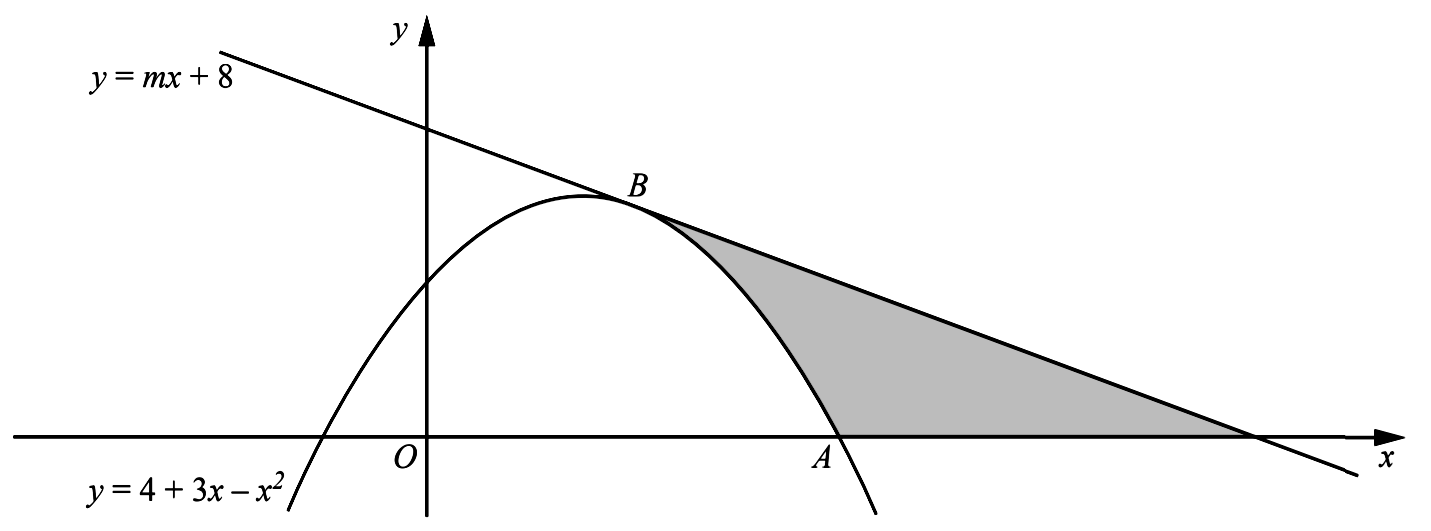
- The diagram shows the curve $y=4+3 x-x^{2}$ intersecting the positive $x$ -axis at the point $A$. The line $y=m x+8$ is a tangent to the curve at the point $B$. Find
- the coordinates of $A$,
- the value of $m$
- the coordinates of $B$,
- the area of the shaded region, showing all your working.
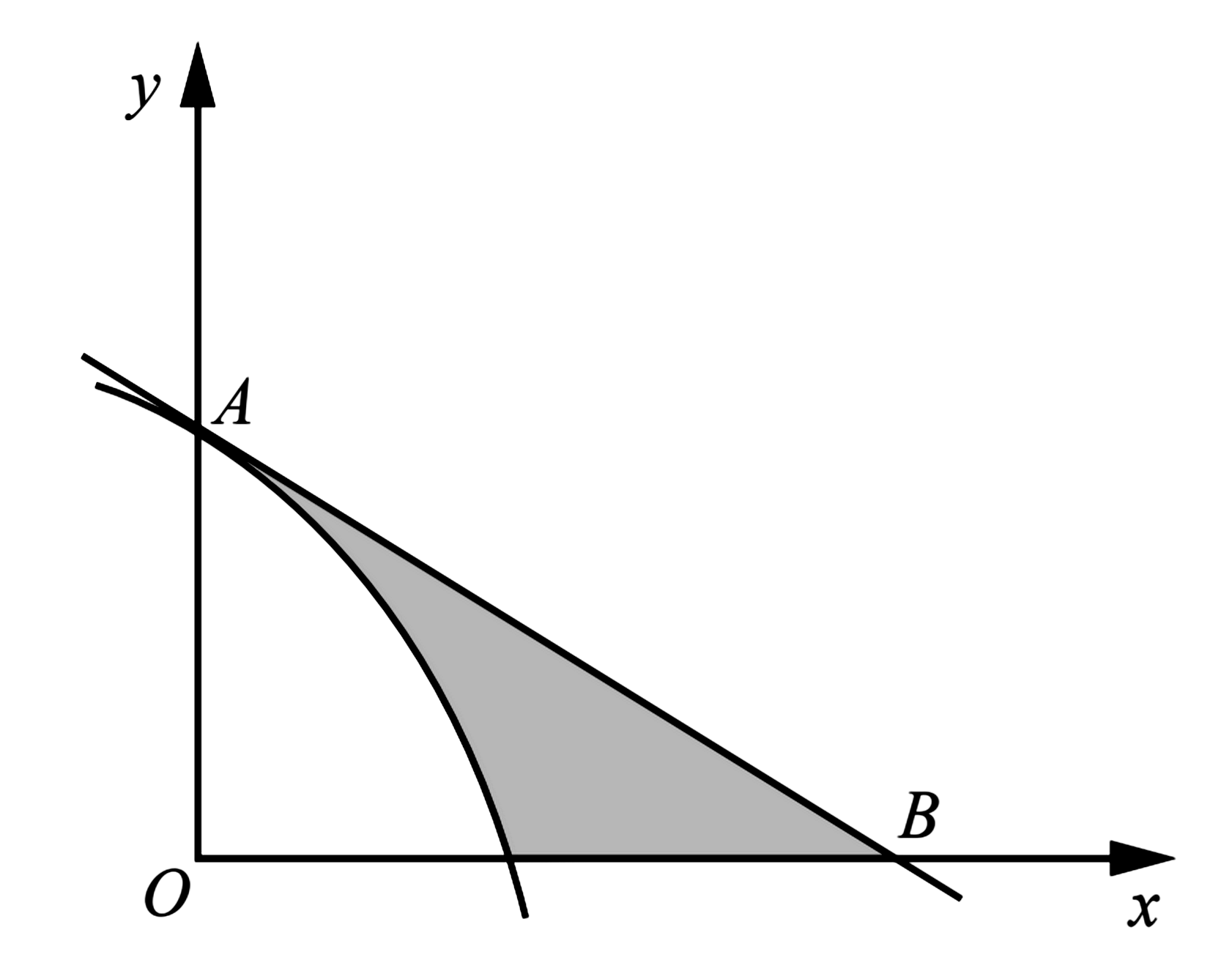
- The diagram shows part of the curve $y=\dfrac{1}{x+1}$. The shaded region $R$ is bounded by the curve and by the lines $x=1, y=0$ and $x=p$.
- Find, in terms of $p$, the area of $R$.
- Hence find, correct to 1 decimal place, the value of $p$ for which the area of $R$ is equal to 2 .
- The diagram, which is not drawn to scale, shows part of the graph of $y=8-\mathrm{e}^{2 x}$, crossing the $y$ -axis at $A$. The tangent to the curve at $A$ crosses the $x$ -axis at $B$. Find the area of the shaded region bounded by the curve, the tangent and the $x$ -axis.
- The diagram shows the curve $y=x^{3}-3 x^{2}-9 x+k$, where $k$ is a constant. The curve has a minimum point on the $x$ -axis.
- Find the value of $k$.
- Find the area of the shaded region.
- The diagram shows the curve $y=x(x-1)(x-2)$, which crosses the $x$ -axis at the points $O(0,0)$, $A(1,0)$ and $B(2,0)$.
- The tangents to the curve at the points $A$ and $B$ meet at the point $C$. Find the $x$ -coordinate of $C$.
- Show by integration that the area of the shaded region $R_{1}$ is the same as the area of the shaded region $R_{2}$
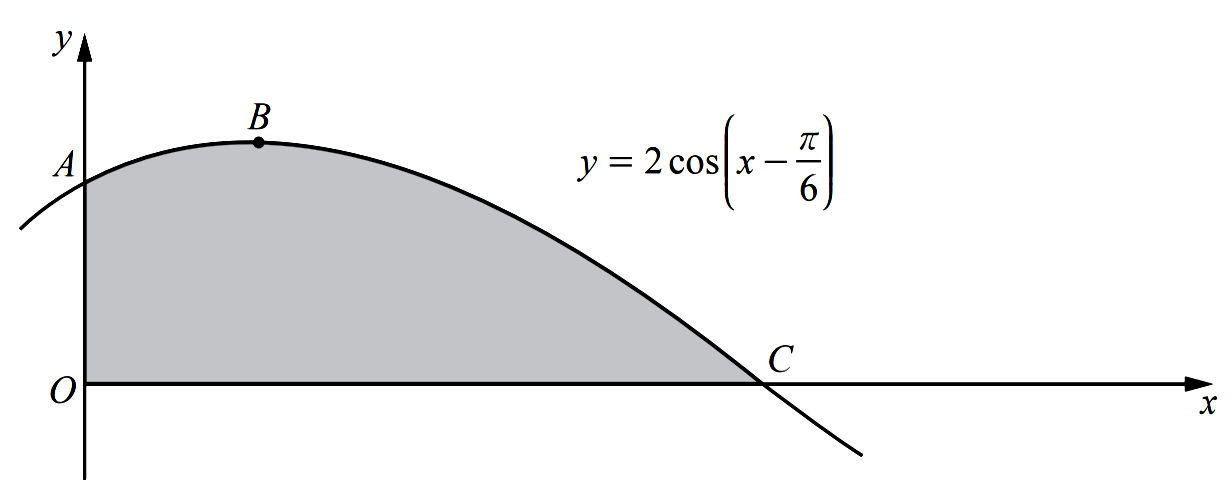
.png)
.png)
.png)













Thank you.
ردحذف